What is Log in Math? Understanding the Basics

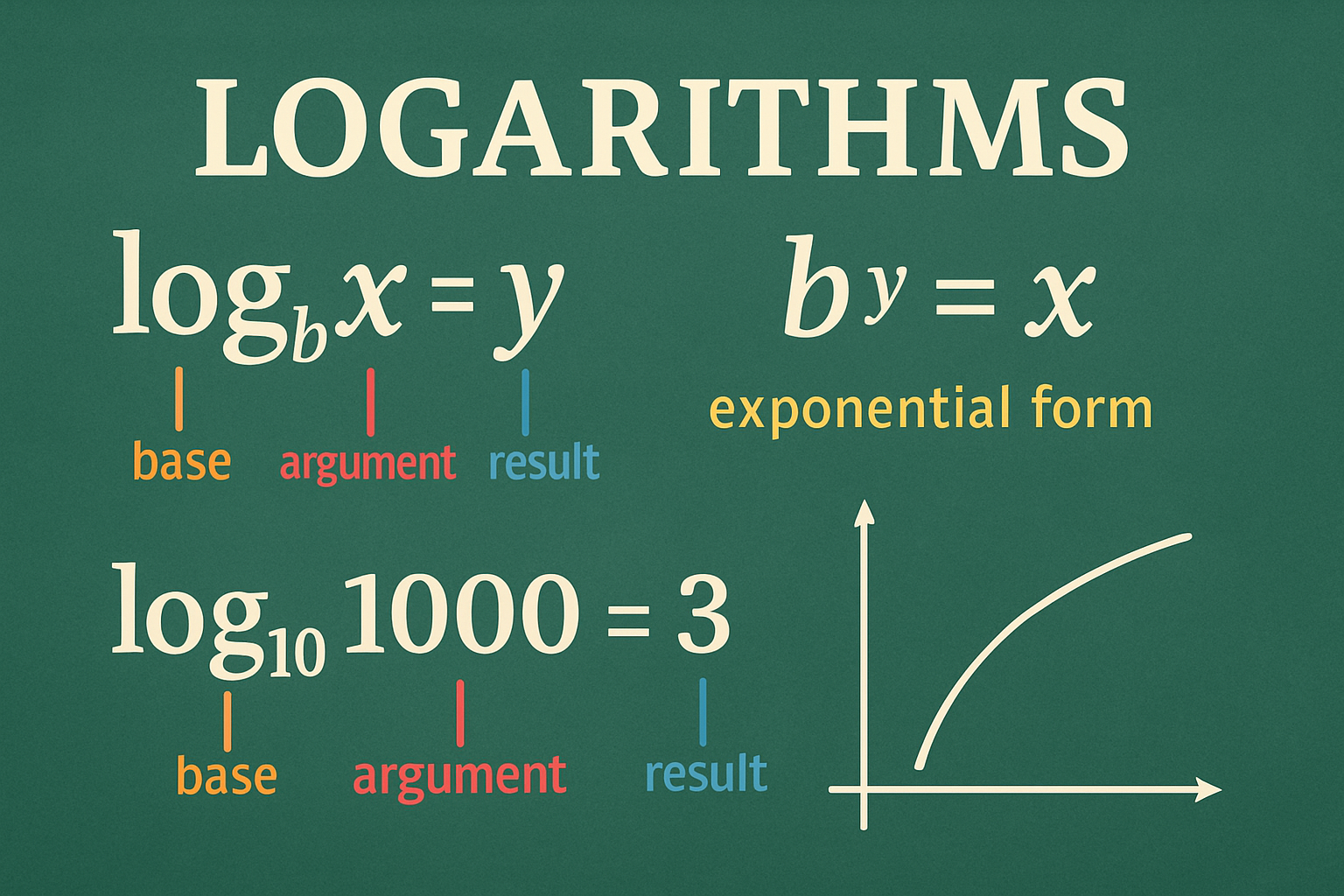
Logarithms (log) are a fundamental concept in mathematics that play a significant role in various fields such as algebra, calculus, and science. They provide a way to solve equations that involve exponential growth or decay. If you've ever encountered a problem that involves multiplying large numbers or dealing with exponential functions, then logarithms have likely appeared.

In this article, we’ll dive into what logs are, why they’re essential, and how they are used in solving equations. Whether you're a student looking to better understand this concept or someone who needs a refresher, this article is for you. We will break down logarithms step by step, making it easier for you to grasp.

What Is a Logarithm?

A logarithm is essentially the inverse operation of exponentiation. This means that while an exponent tells you what power a number must be raised to to get a result, the logarithm does the reverse—it tells you the exponent to which a number (called the base) must be raised to produce a given number.

Example:

In the equation $10^3 = 1000$ , the logarithm of 1000 with base 10 is 3, or $log_{10} 1000 = 3$ .
This is because $10^3$ equals 1000, and so the logarithm tells us what power of 10 must be raised to to get 1000.

Understanding Logarithmic Functions

Logarithmic functions are used to model real-world phenomena, including growth and decay in populations, radioactivity, and financial investments. The general form of a logarithmic equation is:

\log_b(x) = y \quad \text{where} \quad b^y = x

Where:

$b$ is the base of the logarithm
$x$ is the number you're taking the logarithm of
$y$ is the result of the logarithmic operation

For example, if you're solving for $y$ in $log_2 8 = y$ , since $2^3 = 8$ , we know that $y = 3$ .

Types of Logarithms

There are several different types of logarithms, each serving different purposes. The two most common types are:

Common Logarithms (Base 10): These are logarithms where the base is 10. They are often used in scientific calculations because of their ease of use. The common logarithm of a number $x$ is written as $log_{10} x$ , often simply written as $\log x$ .
Natural Logarithms (Base e): These are logarithms with the base $e$ , which is approximately 2.718. Natural logarithms are often used in advanced mathematics, particularly in calculus and in problems involving growth and decay.

Applications of Logarithms

Logarithms have a wide range of applications in many fields. Here are a few examples:

In Finance: Logarithms are used in calculations involving compound interest, growth rates, and in financial modeling.
In Science, Logarithms help in calculating the pH of a solution, measuring sound intensity (decibels), and dealing with seismic data.
In Computer Science, Logarithms are used in algorithms, data structures, and performance analysis, particularly in binary trees and sorting algorithms.